Applied Geometry
Large classes of observed data exhibit complex nonlinear structure. For example, human organs vary nonlinearly in shape, spherical images cannot be analyzed with classical convolutional neural networks due to the curvature of the spherical domain, and particles in a fluid flow interact nonlinearly. Nonlinearity makes geometry a central discipline for modeling dynamics, performing statistical analysis of complex data, and applying machine learning methods to learn from observed nonlinear data.

The research activities in the Applied Geometry group focus on using theory and techniques from the mathematical field of differential geometry to advance data analysis methodology. This happens at a foundational level where fundamental aspects of statistics of nonlinear data are investigated, in applied uses of geometry in e.g. shape analysis of medical and biological data, and on the machine learning side when defining models for neural networks that handles geometric data.
The book Riemannian Geometric Statistics in Medical Image Analysis (Elsevier, 2019) describes many of the complexities and challenges of working with geometric data with a focus on medical applications.
The group is connected to the Center for Computational Evolutionary Morphometry (CCEM) that focuses on shape analysis in evolutionary biology and phylogenetics.
People:
For an updated list of people in the lab, see https://www.ccem.dk/people/.
Shape Analysis
Shapes appear in various forms in medical image analysis and biology, e.g. as 2D surfaces of the human hippocampi or curves representing the outline of a butterfly wing. Analysing the progression of shapes during diseases such as Alzheimer’s disease allows organ shapes to be used as biomarkers for diagnosis and prognosis. Shape analysis also has import application in morphometrics, the study of animal shape changes in biology. More generally, shapes can be considered any object that can be deformed, thus also including complex images such as diffusion weighted MR images in the category of shapes. Mathematically, shape deformations happen by the action of diffeomorphism groups, and geometry of the diffeomorphism groups and its subgroups therefore play important roles in shape analysis. Shape spaces are generally infinite dimensional nonlinear Riemannian manifolds, and statistical shape analysis must thus handle both nonlinearity and infinite dimensionality simultaneously. Focus areas of the work performed in the group is stochastic models for shape evolution and subsequent statistical inference of the parameters governing the stochastically changing shapes. This includes phylogenetic inference using shape data.
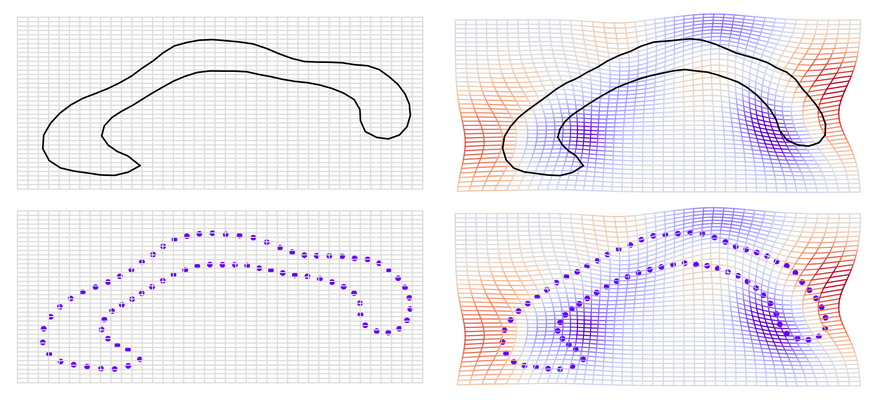
Geometric Statistics
Geometric statistics concerns the statistical analysis of nonlinear data, particularly data residing in geometric spaces such as manifolds. Examples include shapes and shape spaces, tensors as observed in diffusion imaging, protein angles, and directional data. Even the most classical constructions in statistics, e.g. the mean value, are difficult to define in the geometric setting (for the mean, the fact that shapes cannot be added or multiplied by scalars immediately rules out the classic mean estimator of summing observations divided by the number of observations). We focus on probabilistic interpretations of mean values and covariance, and asymptotics of manifold means (central limit theorems of diffusion means). This includes stochastic processes on Riemannian manifolds, and bridge sampling on manifolds and shape spaces.
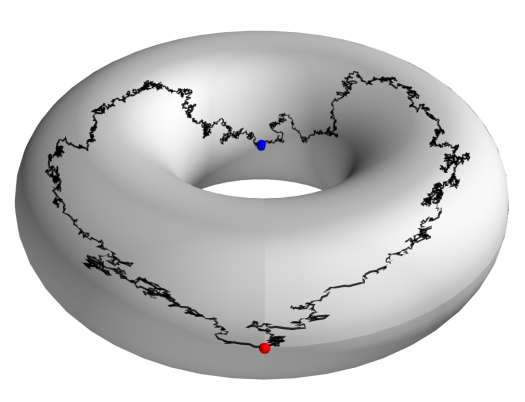
The software packages Jax Geometry and Theano Geometry showcases many of the geometric statistics constructions we work with.
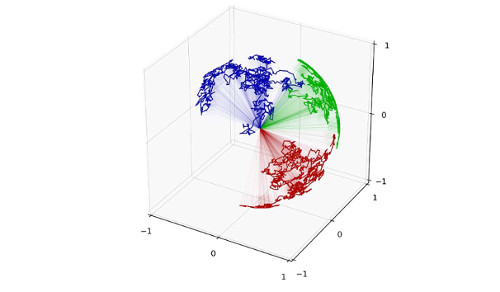
sub-Riemannian geometry
We apply sub-Riemannian constructions for analysis of geometric data, particularly exploring how extremal paths for sub-Riemannian metrics in the frame bundle encode most likely transitions between mean and data points in the presence of non-trivial covariance; how PCA-like dimensionality reduction on manifolds can results in non-integrable distributions and hence allow modelling of higher dimensional data; and reduction theorems on Lie groups and homogeneous spaces for sub-Riemannian metrics.

sub-Riemannian geodesics in the frame bundle FM of a manifold M represented most probable paths between data mean and samples with different covariance structures.
Geometric Deep Learning
Convolutional neural networks classically take image on 2D domains as input. Geometric deep learning aims at extending the class of input data to allow curved domains or more general data with geometric structure. We tackle both foundational questions in geometric deep learning such as the definition of convolution operators on geometric domains and application of geometric deep learning methods in specific contexts such as for diffusion weighed images.
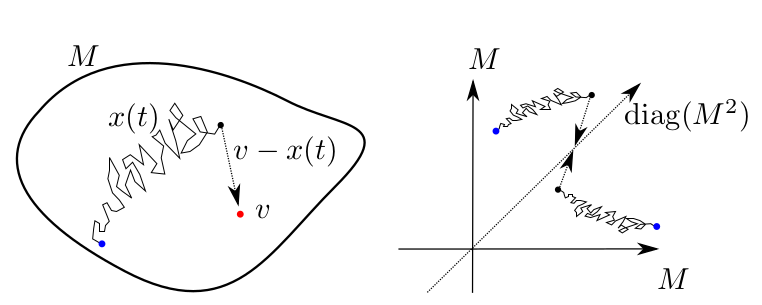
Bridge sampling techniques for defining manifold valued convolution operators.
Current Research Projects
Stochastic Morphometry: Evolutionary Modeling of Whole Shape Data (2022-2025)
Villum Foundation
Stefan Sommer, Rasmus Nielsen, Mads Nielsen and Christy Hipsley
Probabilistic Shape Statistics (2019-2023)
Novo Nordisk Foundation
Led by Stefan Sommer
Completed Research Projects
Daydreaming Algorithms (2019-2021)
VILLUM Foundation Experiment Programme
Led by Stefan Sommer
To take on master level projects in applied geometry, a solid mathematical background is needed. We generally mix machine learning, statistics and probability theory with geometry making the machine learning and advanced machine learning courses at DIKU very relevant (e.g. Introduction to Machine Learning / Machine Learning A + B, Artificial Intelligence / Advanced Deep Learning, Machine Learning, Advanced topics in Machine Learning). UCPH courses focusing on geometry include Geometri 1, Geometry 2, Riemannian Geometry and General Relativity, Analysis on Manifolds. Courses on mathematical statistics and probability theory are also very relevant, e.g. Stokastiske processer.
- Math on Long Island, July 2022
- Workshop on Stochastic Morphometrics, June 8-10 2022
We participate in international networks and fora including
- MICCAI Special Interest Group in Shape Modeling and Analysis in Medical imaging (ShapeMI)
- Math in the X workshops, see e.g. Math on the Rocks or Math in the Black Forest
- International Shape Statistics Group organized by Professor Stephen Pizer and Sungmin Hong
Online available talks and presentations:
- ShapeMI2020 Keynote "Stochastic Shape analysis and Probabilistic Geometric Statistics" (video)
- "Statistical Inference in Nonlinear Spaces via Maximum Likelihood and Diffusion Bridge Simulation", Isaac Newton Institute for Mathematical Sciences, 2016 (video)
People
| Name | Title | Phone |
|---|
Contact
 Stefan Sommer
Stefan Sommer
Professor
sommer@di.ku.dk
